Merge Sort

Sorting Algorithms

A Divide and Conquer Algorithm

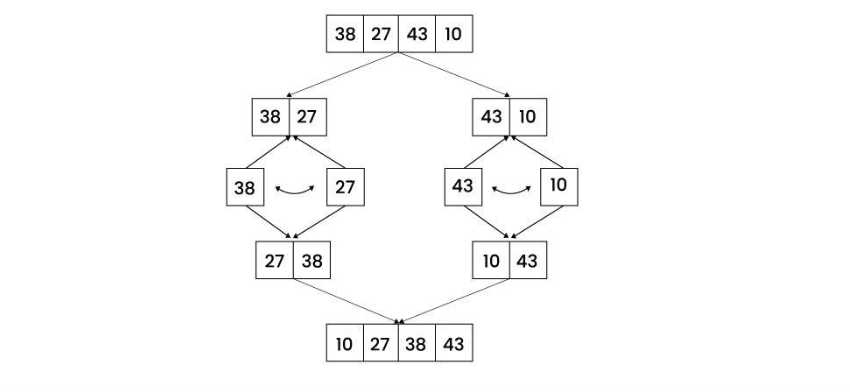
At a high level, we will use Recursion by sorting the left half, sort the right halt, and then merge those two sorted halves together.

Whats funny is that you don’t have to do any explicit sorting of the halves, through recursion, we will start with sorted singleton lists and then the sorting happens in the ‘merge’ into more sorted lsit, which we in turn merge.

void mergeSort(vector<int> &arr){
	recursiveMergeSort(arr, 0, arr.size()-1);
}
 
  
 
void recursiveMergeSort(vector<int> &arr, int leftStart, int rightEnd){
	// base
	if (leftStart >= rightEnd){
		return;
	}
	int mid = (leftStart + rightEnd)/2;
	recursiveMergeSort(arr, leftStart, mid); // sort the left
	recursiveMergeSort(arr, mid+1, rightEnd); // sort the right
	mergeHalves(arr, leftStart, mid, rightEnd);
}
 
  
 
void mergeHalves(vector<int> &arr, int leftStart, int mid, int rightEnd){
 
// merge in place on arr
 
// treat two halves as iteration through two pointers
 
int n1 = mid + 1 - leftStart;
 
int n2 = rightEnd - mid;
 
  
 
// Create temp vectors
 
vector<int> L(n1), R(n2);
 
  
  
 
// Populate temp vectors with copies of the two sorte halves to merge.
 
for (int i = 0; i < n1; i++){
 
L[i] = arr[leftStart + i]; // leftStart offset
 
}
 
for (int i = 0; i < n2; i++){
 
R[i] = arr[mid + 1 + i]; // rightStart offset
 
}
 
  
  
 
// merge the two vectors onto arr
 
int i = 0, j = 0;
 
int k = leftStart;
 
while (i < n1 && j < n2){
 
cout << "k: " << k << " i: " << i << " j: " << j << endl;
 
// both L[i] and R[j] avaliable
 
if (L[i] < R[j]){
 
arr[k] = L[i];
 
i++;
 
} else {
 
arr[k] = R[j];
 
j++;
 
}
 
k++;
 
}
 
  
 
// copy remaining elements of L[] if any
 
while (i < n1){
 
arr[k] = L[i];
 
i++;
 
k++;
 
}
 
  
 
// copy remaining elements of R[] if any
 
while (j < n2){
 
arr[k] = R[j];
 
j++;
 
k++;
 
}
 
}
 
};

Complexity

Time complexity: $O(n\log n)$ – efficient and consistent.

Space complexity: $O(n)$ – main drawback vs. Bubble Sort’s $O(1)$.

• Merging two halves requires extra space.
• To optimize, recursiveMergeSort can be a void function: sort left and right halves in place, then merge into a new array.
• Still $O(n)$ overall, since merging requires allocating a temp array of size $n$ at each level of recursion.