Recursion

Theorem

Anything recursive can me implemented iteratively, without recursion.

Ingredients:

1. Base case: conditions that terminate the recursion, an explicit value, state variable is returned with no recursive calls.
2. return a function of the recursive call. answer, passing in a parameter that moves execution closer to a halt, is it doesnt grow the problem, the solution space, it reduces it ensuring the process will reach/converge tot he base case.

void fun(int state){
	// Base Case
	if (basecase(state)){
		return literal;
	}
	// Recursive call
	return g(fun(y))
}

Case study, fibonacci

# REcursive
int fib(int n){
	if (n == 1){
		return 1;
	} else if  (n == 2){
		return 2;
	} 
	return fib(n-1)+fib(n-2);
}
 
 
# iterative 
int fib_iter(int n){
  int myarr[n];
  if (n < 3 && n > 0) return n;
  myarr[0] = 1;
  myarr[1] = 2;
  for (int i = 2; i < n; i++){
	  myarr[i] = myarr[i-1] + myarr[i-2];
  }
  return myarr[n-1];
}
 
 

Inefficiencies

A source of inefficiency is that it has a tendency to recompute several values. In the naive fibonacci implementation, the two recursive calls open up a binary tree structure, setting the base complexity at exponential time, without prior

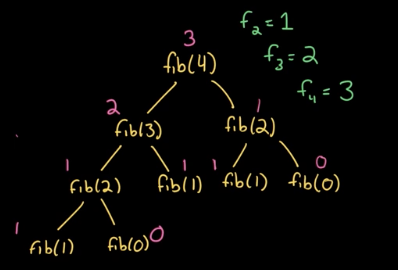
The solution is caching, once you have computed fib()

memoization

if you store the result of fib(2) after computing it recursiveley for the first time, you avoid the computation on the right sub tree.

int fib(int n, map<int,int> memz){
	if (n <= 2 && n > 0) return n;
	fib1 = (memz.find(n-1) == memz.end()) ? fib(n-1) : memz[n-1]
	fib1 = (memz.find(n-2) == memz.end()) ? fib(n-2) : memz[n-2]
	return fib1+fib2;
}

The map from integers to integers seems kinda superfluous, as this is essentially a vector, but its meant to represent that you can map any sort of input to its cached/memoized value.

By returning stored values for previously computed inputs we can actually cut the time from exponential to linear, a massive improvement using memoization.

Space Complexity of the Naive Fibonacci Algorithm

The space complexity of the naive recursive Fibonacci algorithm is not O(2n)O(2^n)O(2n). That might seem counterintuitive at first—after all, the time complexity is O(2n)O(2^n)O(2n), so it’s easy to assume the space usage would be the same. But that’s not how space complexity works.

Quick reminder:
Think of space complexity as “how big a chunk of memory you need to run your code at any point in time.”

In recursive algorithms, the call stack does contribute to space usage, but crucially, not all recursive calls exist on the stack at the same time. Once a recursive branch completes and returns, it frees up its stack frame.

In the case of naive Fibonacci, the maximum stack depth corresponds to the deepest path from the initial call down to a base case—essentially a straight line of recursive calls. This depth is O(n)O(n)O(n), so the space complexity is O(n)O(n)O(n), not exponential.

So what’s really happening?

• At any given moment, the call stack only holds the current recursive path (the “dive to the bottom”).

• Once we hit a base case and return, that space is freed.

• We never have all O(2n)O(2^n)O(2n) calls alive in memory at once—just one path’s worth, which is linear in size.

In summary:
✔️ Time complexity = O(2^n) (due to repeated calculations)
✔️ Space complexity = O(n)(due to the call stack depth)

And of course its the same space complexity for the memoized solution.

State

I like passing as argument a bunch of state variables, or a state structures by reference and mutate them in place, meaning your recursive function could even be void.

You can avoid to pass many state variables as argumetns, by computing metrics for your children (bellow) and then passing them up to your parent at every node, exactly like in fibo above, or like so:

int countPaths(vector<vector<int>> &grid, int n, Coordinates position = {0,0}){	
	// count = 0 essentially means you are counting paths 'below,'
	
	// or stemming from the current state through your children, then you pass the count up to your parent.
	
	int count = 0, x = position.first, y = position.second;
	
	
	// base cases:
	
	// 1. isAtEnd() => if you are at the end of the grid and on a safe cell
	if (x == n-1 && y == n-1 && grid[x][y] == 0) return 1;
	
	// 2. !validSquare() => if your position is lava or if you are trapped with lava on both sides
	if (grid[x][y] == 1 || (x + 1 < n && grid[x+1][y] == 1) && (y + 1 < n && grid[x][y+1] == 1)) return 0;
	
	// recursive cases:
	
	// 1. move down
	if ( x + 1 < n && grid[x+1][y] == 0){
		count += countPaths(grid, n, {x+1,y});
	}
	// 2. move right
	if ( y + 1 < n && grid[x][y+1] == 0){
		count += countPaths(grid, n, {x,y+1});
	}
	
	return count;
 
}

Paths

If you want to keep track of the recursive paths, you will need to continuously copy the current path into a new path to which you can add the current state. This adds to the time complexity, but you can keep track of exact cycles, coin change seqeunces, and any other recursive path.